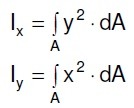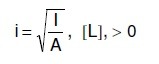Geometrijske karakteristike poprečnog preseka

Beleške > Mašinstvo > Otpornost materijala > Geometrijske karakteristike poprečnog preseka

Objavljeno / 13.09.2012. Autor / Milena Ristić Kategorija / Otpornost materijala

Poprečni presek – figura ili slika u presečnoj ravni koja je upravna na podužnu osu štapa, odnosno, na srednju površ posmatranog konstruktivno elementa.
Geometrijska karakteristika – definiše poprečni presek i zavisi od njegovog oblika i položaja u prostoru.

1. Površina poprečnog preseka

– uvek je veća od nule, A>0
– dimenzija je L² [cm²], gde je L – dužina

2. Statički moment površine poprečnog preseka

– zamišljena geometrijska karakteristika
– predstavlja proizvod veličine površine date figure i rastojanja njenog težišta do ose u odnosu na koju se ova veličina izračunava

– može biti veći, manji ili jednak nuli, S>0, S<0, S=0
– dimenzija je L³
– zavisi od toga kakav je položaj poprečnog preseka u odnosu na koordinatni početak
– za osu koja je osa simetrije poprečnog preseka, statički moment će biti jednak nuli.
– za težišnu osu poprečnog preseka, statički moment je jednak nuli
– za celu površinu A:

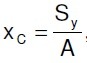, koordinata x: , koordinata y:

3. Aksijalni momenti inercije poprečnog preseka

– momenti inercije površine A za ose x i y.
– zamišljena geometrijska karakteristika
– dimenzija je L⁴
– uvek je veći od nule
– zamišljeni otpor poprečnog preseka na savijanje

4. Centrifugalni moment inercije površine A za par međusobno upravnih osa (x i y)

– zamišljena geometrijska karakteristika
– dimenzija je L⁴
– može biti manja, veća ili jednaka nuli
– ako poprečni presek ima bar jednu osu simetrije, za tu površinu i za taj par osa, centrifugalni moment jednak je nuli.

5. Polarni moment inercije

– moment inercije površine A za tačku O (pol O), odnosno, za osu z upravnu na ravan xy
– zamišljena geometrijska karakteristika
– dimenzija je L⁴
– uvek je veći od nule
– ne zavisi od izbora koordinatnog sistema (invarijantan je)
– jednak je zbiru dva aksijalna momenta inercije za bilo koji par ortogonalnih osa koje prolaze kroz isti pol O
– zamišljeni otpor poprečnog preseka na uvijanje

PROMENA MOMENATA INERCIJE PRI TRANSFORMACIJI KOORDINATNOG SISTEMA

Translacija koordinatnog sistema

– veza izmedju koordinatnih sistema xy i ξη: ξ = a + x , η = b + y
– ukoliko je koordinatni sistem težišni, statički momenti su jednaki nuli.

– a = ξc i b = ηc, pa prethodni izrazi postaju:

i to su Štajnerovi obrasci, pri čemu ćemo se osloniti na prostiju predstavu formula:
momenti inercije = težišni (sopstveni) momenti inercije + položajni momeni inercije

– Štajnerova teorema: Moment inercije za proizvoljnu osu, jednak je zbiru momenata inercije za težišnu osu (koja je paralelna toj proizvoljnoj osi) i položajnog momenta inercije.

– aksijalni moment inercije za težišnu osu uvek je manji od momena inercije za bilo koju drugu osu paralelnu težišnoj

Rotacija koordinatnog sistema

– veza izmedju koordinata dva koordinatna sistema:

– dovoljno je poznavati momente inercije za dve međusobno upravne ose da bi se mogli odrediti momenti inercije za bilo koje druge dve međusobno upravne ose koje prolaze kroz isti koordinatni početak.

GLAVNI TEŽIŠNI MOMENTI INERCIJE

– Glavni težišni momenti inercije menjaju se u zavisnosti od ugla.
– 1 i 2 su glavne ose inercije, a odgovarajući mmenti inercije, glavnim momentima inercije
– ako je koordinatni početak u težištu poprečnog preseka, ose 1 i 2 nazivaju se glavne težišne ose inercije, a momenti inercije I1 i I2 su glavni težišni momenti inercije.
– glavni težišni koordinatni sistem je onaj težišni koordinatni sistem za čiji je par osa centrifugalni moment inercije jednak nuli, a aksijalni momenti inercije imaju ekstremne vrednosti.

POLUPREČNICI INERCIJE