Spreg sila

Slaganje dveju paralelnih sila

• može se pokazati da ovaj sistem sila može zameniti jednostavnijim, njemu ekvivalentnim sistemom sučeljnih sila za koji se zna da ima rezultantu. 
• sistem od dve paralelne sile istog smera, koje deleuju na telo, ima rezultantu čiji je intenzitet jednak zbiru intenziteta komponenata, koja je istog smera kao i komponente, i koja se nalazi bliže sili većeg inetenziteta na rastojanju koje je određeno sa

 

Sistem od dve paralelne sile, različitih intenziteta i smerova, koje deluju na telo, ima razultantu čiji je intenzitet jednak razlici intenziteta komponenata, koja je usmerena u stranu sile većeg intenziteta, i koja se nalazi sa strane veće sile na rastojanju koje je odrađeno sa  

Spreg sila

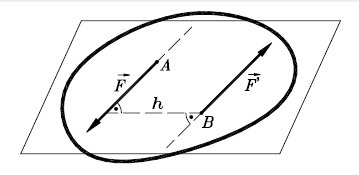
Sistem od dve paralelne sile jednakih intenziteta, suprotnih smerova, čije se napadne linije nalaze na konačnom rastojanju, naziva se spreg sila .
Ravan određena napadnim linijama sila sprega, naziva se ravan dejstva sprega sila.
Najkraće rastojanje h između napadnih linija sila sprega naziva se krak sprega.
Obrtno dejstvo sprega sila zavisi od :
– intenziteta sila sprega i kraka sprega.
– položaja ravni dejstva sprega sila
– smera obrtanja u ravni dejstva sprega sila
Spreg sila može biti definisan jednim vektorom, u tom cilju uvodi se moment sprega sila.

Moment sprega sila je definisan na sledeći način :
– intenzitet momenta sprega sila jednak je proizvodu intenziteta sile F i kraka sprega sila h, M=F*h.
– pravac momenta sprega sila upravan je na ravan dejstva sprega sila.
– smer momenata sprega sila je na onu stranu odakle se obrtno dejstvo sprega sila vidi kao matematički pozitivno.

(5.38, 5.39, 5.40, 5.41, 5.42)

Glavni moment sila sprega jednak momentu jedne sile za tačku na napadnoj liniji druge sile. Glavni momenat je i slobodan vektor jer ne zavisi od izbora momentne tačke.

Intenzitet glavnog momenta sprega sila  5.44, 5.45

Pravac glavnog momenta sprega sila upravan je na ravan dejstva sprega sila.
Smer glavnog momenta sprega sila je na onu stranu prostora odakle se obrtanje vektora AB najkraćim putem do poklapanja sa vektorom F, vidi kao matematički pozitivno.
Intenzitet , pravac i smer glavnog momenta sprega sila odgovara vektoru momenta sprega sila M. sl 47

Ekvivalentnost spregova sila

Teorema 1 : Dejstvo datog sprega sila na telo neće se promeniti ako se taj spreg sila zameni bilo kojim drugim spregom sila koji ima istu ravan dejstva, isti smer i intenzitet momenta sa polaznim spregom sila.sl 48a, 5.46, 5.47, 5.48, 5.49, 5.50

Na osnovu Varinjonove teoreme o momentu reziltujićih sečeljnih sistema sila 5.51

Teorema 2 : Dejstvo datog sprega sila na telo neće se promeniti ako se taj spreg sila prenese iz njegove ravni dejstva u bilo koju drugu paralelnu ravan.
Moment sprega sila koje deluju na telo , kao mera dejstva sprega sila, je slobodan vektor i da se može preneti u bilo koju tačku tela zadrži njegov pravac, smer i intenzitet.

Slaganje spregova sila

Koristeći teoremu o slobodnom pomeranju spregova sila u ravni svog dejstva, spreg sila (P1,P1′) mogu se zameniti sa (F1,F1′), a (P2, P2′) sa (F2,F2′) ovim postupkom dobijena su dva sprega sila (F1,F1′) i (F2, F2′) koji imaju zajednički krak AB. 5.60, 5.62, 5.64

Moment spregova polaznog sistema spregova sila 5.65, 5.66

Moment novodobijenog sprega sila5.67, 5.68

Moment rezultujućeg sprega sila, sistem spregova sila, jednak je vektorskom zbiru momenata komponentalnih spregova sila, odnosno predstavlja glavni moment sistema spregova sila. sl 50, 5.69, 5.70

Moment razultujućeg sprega sila, ravnog sistema spregova sila je vektor koji ima projekciju samo na osu upravnu na ravan dejstva svih spregova sila, pri čemu je ta projekcija jednaka zbiru projekcija momenata komponentalnih spregova sila na istu osu. sl 51

Uslovi ravnoteže sistema spregova sila

Potreban i dovoljan uslov da bi prostorni sistem spregova sila bio uravnotežen, jeste da je vektorski zbir momenata svih spregova sila jednak nuli. 5.77